第1回実験

はじめに
- 位置決め制御とは？
- フィードバック制御とは？
実験
レポート課題

はじめに

「制御工学」の実験では，講義内容を確認するための実験だけでなく，むしろ今後の講義の基礎となるような現象・状況を体験する実験を主に行います．第一回目では制御系に求められる具体的な指標を確かめ，制御系設計の面白さや難しさを実感します．

　コア実験は資料を見ながら各自で進めます．最後に20分間程度の説明を行いますので，この資料の実験は90分程度で終わるように時間配分を考えて実験を行って下さい．わからない点などがあれば教員やTAに質問して下さい．

位置決め制御とは？

対象の物理量を与えられた目標に追従させる制御，すなわち目標値追従制御は制御の重要な目的の一つです．とくに機械の制御では，目標値追従制御の一種である「位置決め制御」と呼ばれる制御がよく行われます．「位置決め制御」とはロボットの腕や機械装置を，あらかじめ定められた角度や位置に移動させて，維持させる制御です．初回の講義で体験した実験は角度に関する位置決め制御です．位置決め制御はフィードバック制御の目的としては最も単純なものですが，最も多く使われている制御です．エレベータが各階で停止するのも位置決め制御の例です．

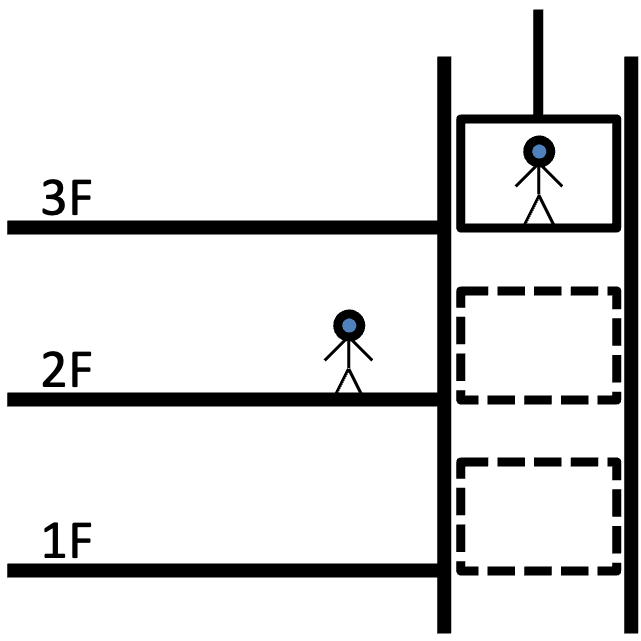
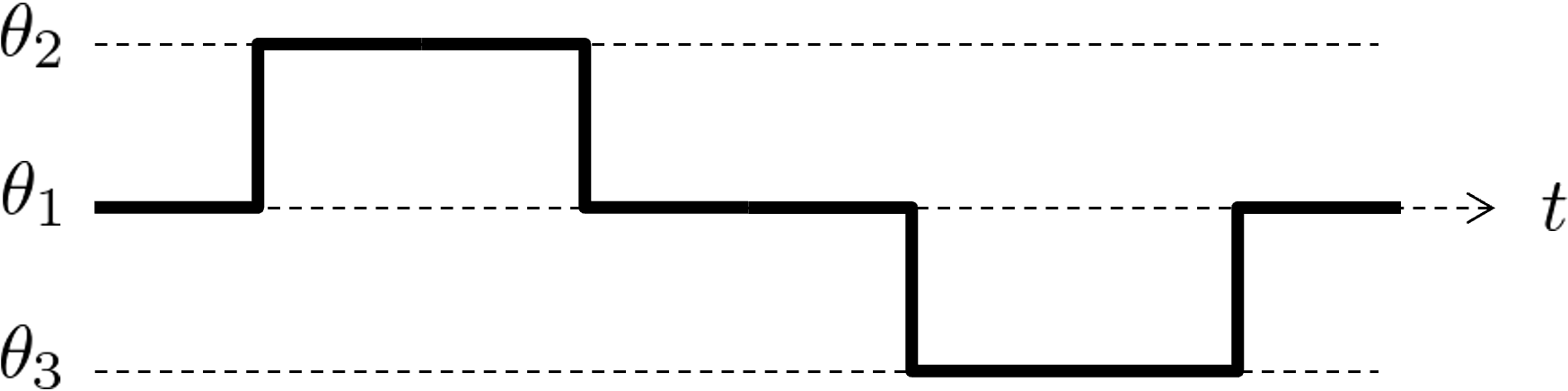
位置決め制御では，対象物体の角度・位置を目標とする角度・位置に，すばやく正確に制御することが求められます．目標角度・位置は各時刻で例えばつぎのように与えられます．下記は目標が時間とともに \(\theta_1\) → \(\theta_2\) → \(\theta_1\) → \(\theta_3\) → \(\theta_1\) と変化する様子を示しています．位置決め制御では目標通りに機械が動作することが理想です．

今回のコア実験では，位置決め制御実験を通してフィードバック制御の概要，フィードバック制御系の設計の課題などを把握します．使用する実験装置は初回の講義で使用した実験装置と同じものです．

フィードバック制御とは？

初回の講義で説明されたように，フィードバック制御は目標と現在の状況との差に基づいて操作量（電圧，トルクなど）を定めます．操作量は制御入力とも言われます．その関係を図にすると下図のようになります．各時刻 \(t\) で目標 \(r(t)\) が与えられます．コントローラは各時刻で \(r(t)\) と現在の出力（角度，位置など） \(y(t)\) との差 \(e(t) = r(t) – y(t)\) を計算し，その差に応じて制御入力 \(u(t)\) を計算します．制御入力 \(u(t)\) が対象に作用すると対象が何らかの運動を行い，出力 \(y(t)\) が変化します．上記の動作を時々刻々繰り返すのがフィードバック制御です．差 \(e(t)\) をとくに偏差と言います．

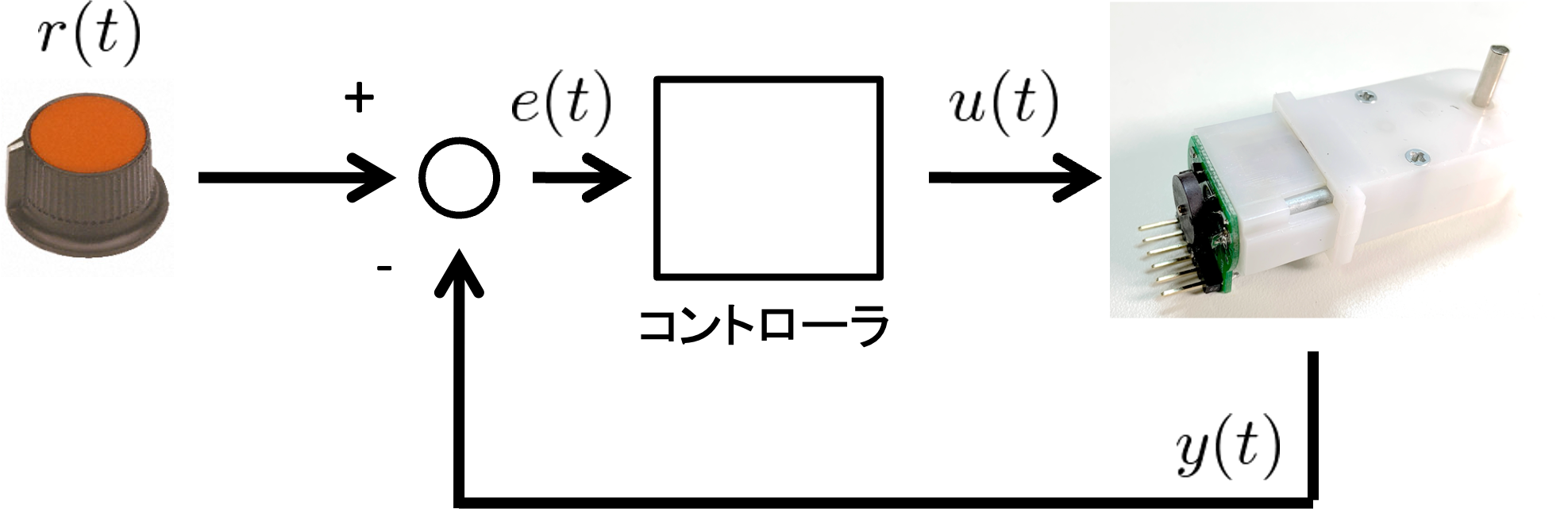
フィードバック制御では \(u(t)\) を定めるための計算規則が重要な役割を果たします．この計算規則を制御則とよびます．

最も簡単な制御則は \(u(t)\) を \(e(t)\) に比例して与えるものです．式で書くと次式のようになります．

\[\Large{ \begin{align} u(t) = K_p e(t) \end{align} }\]

上記の制御則は偏差に比例して制御入力を定めるので比例制御と言われています．Proportional（比例）の頭文字をとって P 制御とよばれることもあります． \(K_p\) は比例定数で，とくに比例ゲインとよばれています．

それではまず，比例制御でどこまで目標を達成できるのか実験してみましょう．今回用いる実験装置は初回の講義で用いたものと同じものです．この実験装置の出力 \(y(t)\) はアームの角度，制御入力 \(u(t)\) はモータへの印加電圧です．

Feedback制御実験を開いてください．別タブで開きます．

実験

実験準備

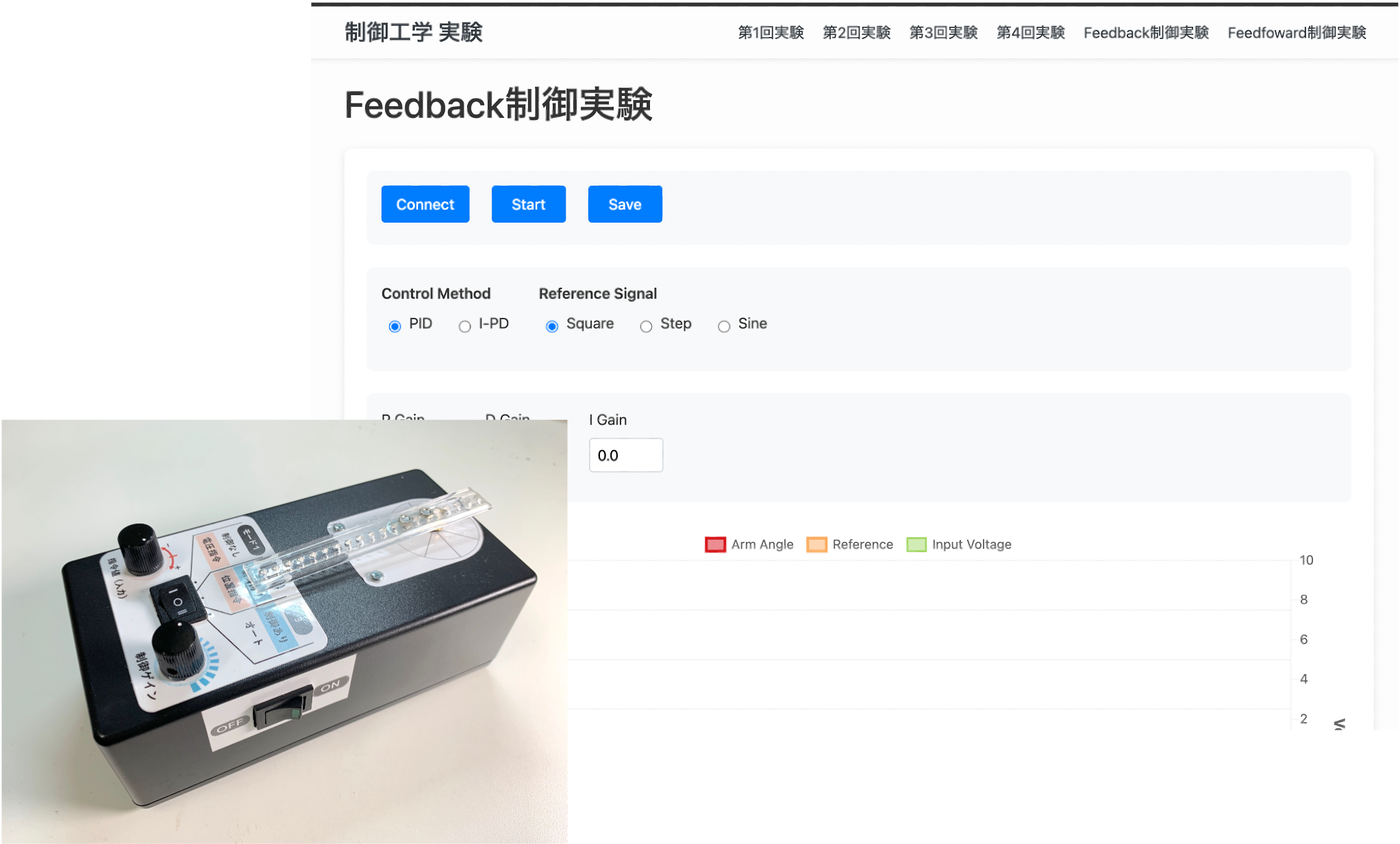
別タブに，下図の画面が表示されているはずです．この画面の操作によって制御実験を行います．

まずは，“connect”をクリックし，実験装置が接続されているUSBポートを選択します．Windowsの場合は，”COM**“，Macの場合は，”/dev/cu.usbserial” などが選択できると思います．できない場合は，実験準備を参考にドライバーをインストールしてください．接続できたら，connectボタンが緑色に変わります．

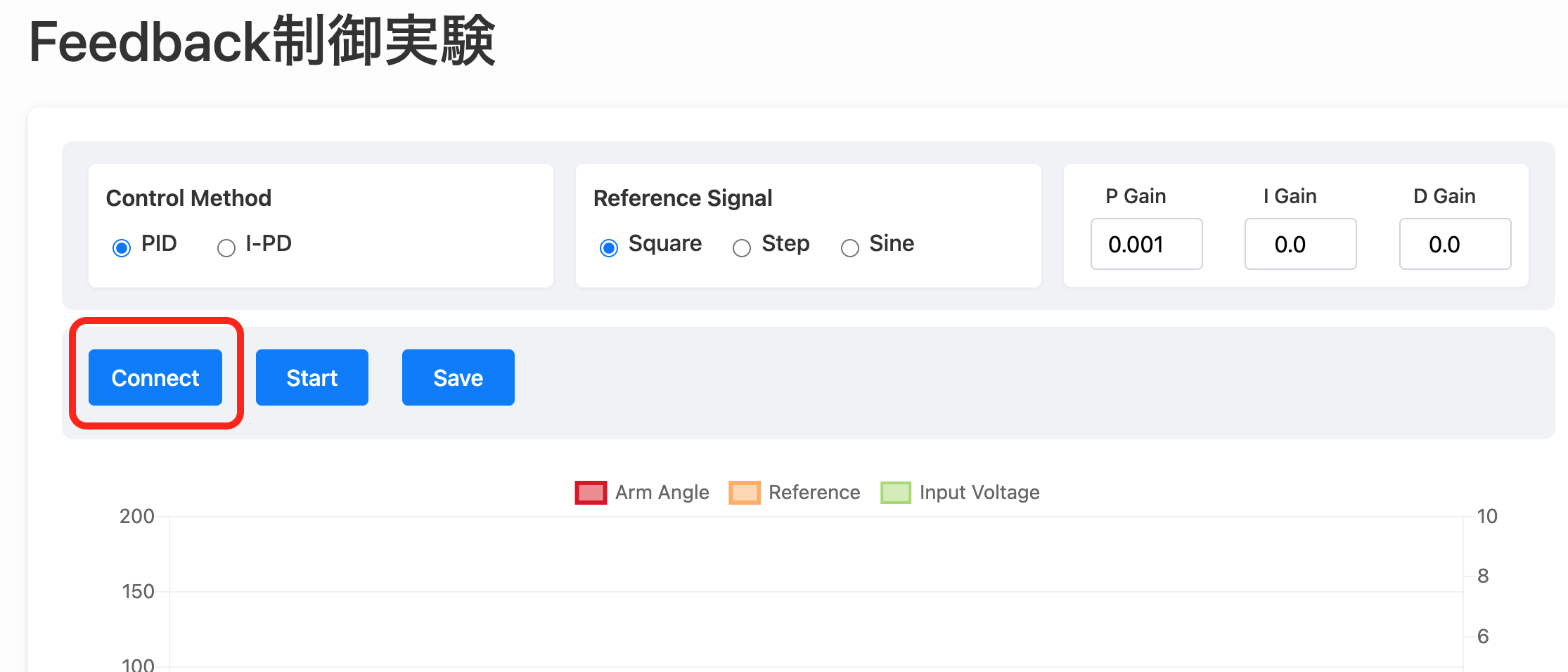
比例制御（P制御）実験

画面の各部を説明します．”start”ボタンによって実験を開始，”stop”ボタンで停止します．左の”P gain”と書かれた欄で比例ゲインを設定します．“I gain”，”D gain” の部分は後で説明します．下のグラフ部分に実験結果が表示されます．

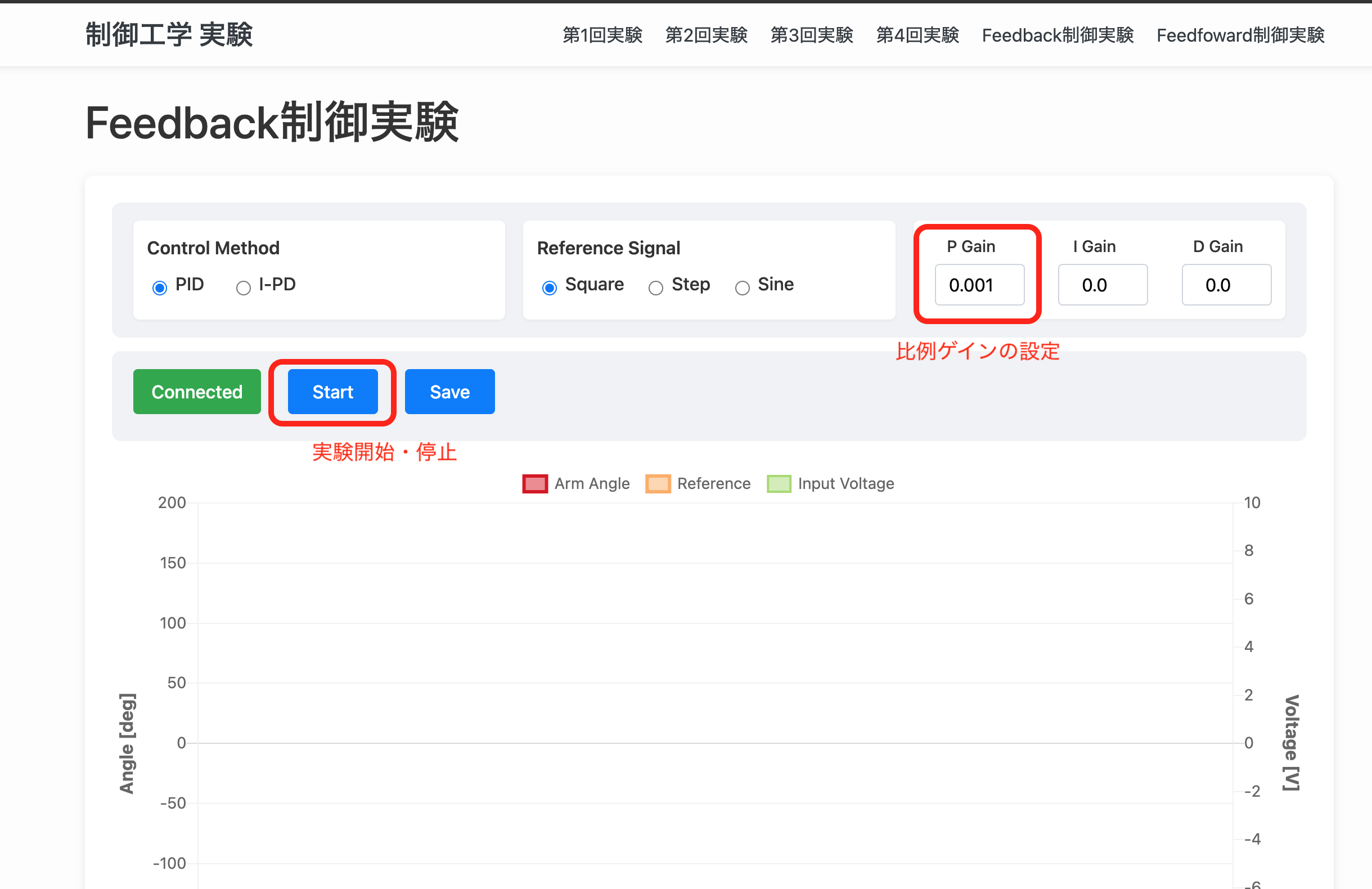
早速実験を行ってみましょう．比例ゲインは 0.001 に設定されています．このまま，画面の”start”をクリックして下さい．実験が始まります．”stop”ボタンをクリックすると実験は停止します．

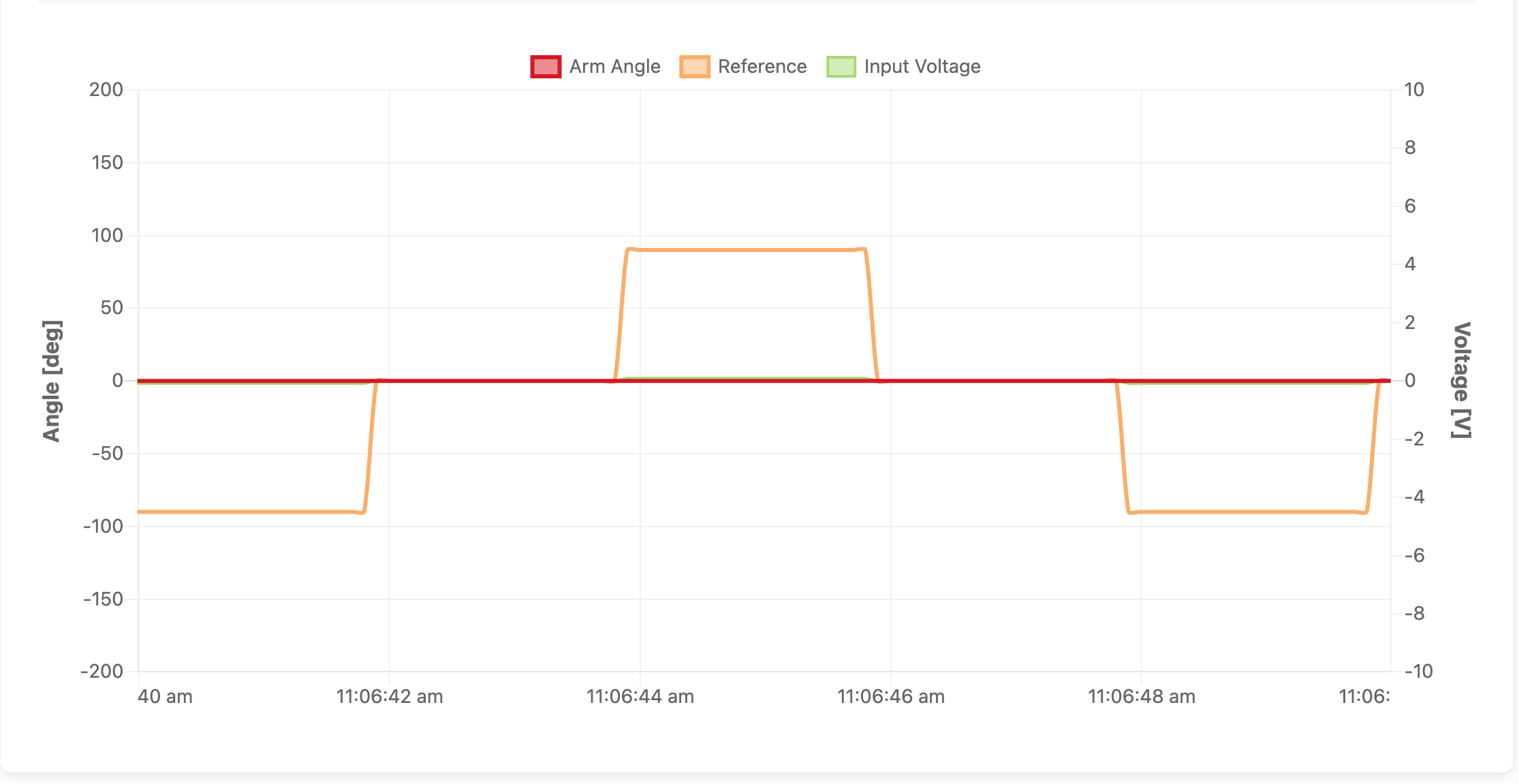
実験を開始すると画面には下記のようなグラフが表示されるはずです．グラフの横軸は時間，縦軸は角度です．オレンジの線は目標角度を示しています．この実験装置では目標角度はプログラムであらかじめ与えています．具体的には2秒おきに \(0\) → \(\pi/2\) → \(0\) → \(-\pi/2\) を繰り返す目標を与えています．

一方，赤のグラフはモータの角度，緑のグラフはモータへの印加電圧を示しています．目標角度と実際の角度の間に偏差が生じていて，なおかつ比例ゲインは0ではないので制御入力（モータへの印加電圧）も0ではありません．しかしながら，実際にはモータ角度は変化していません．これはモータ軸にマサツがあるためです．今のゲイン設定では発生するトルクが小さすぎてマサツに打ち勝つことができません．そのためモータは動きません．

この比例ゲインではマサツに負けてしまうので，トルクを大きくするために比例ゲインを大きくしてみましょう．一度，”stop”をクリックし，比例ゲインを0.01程度にして下さい．その後”start” をクリックすると設定したゲインで制御が行われるようになります．モータが動き出しましたか？　もし動かなければ，比例ゲインを0.02程度に増やして試してみましょう．

比例ゲインを0.1程度にするとモータが何らかの動きをするはずです．最初に位置決め制御（目標値追従制御）の理想は目標と全く同じ動作をすることだと書きましたが，その通りなっているでしょうか？実際にはそうなっていないはずです．装置の個体差によって多少の違いはありますが，おおよそ下図のような結果になっているのではないでしょうか．下図の紫の結果のように，何らかの入力に対する出力を一般に応答と言います．

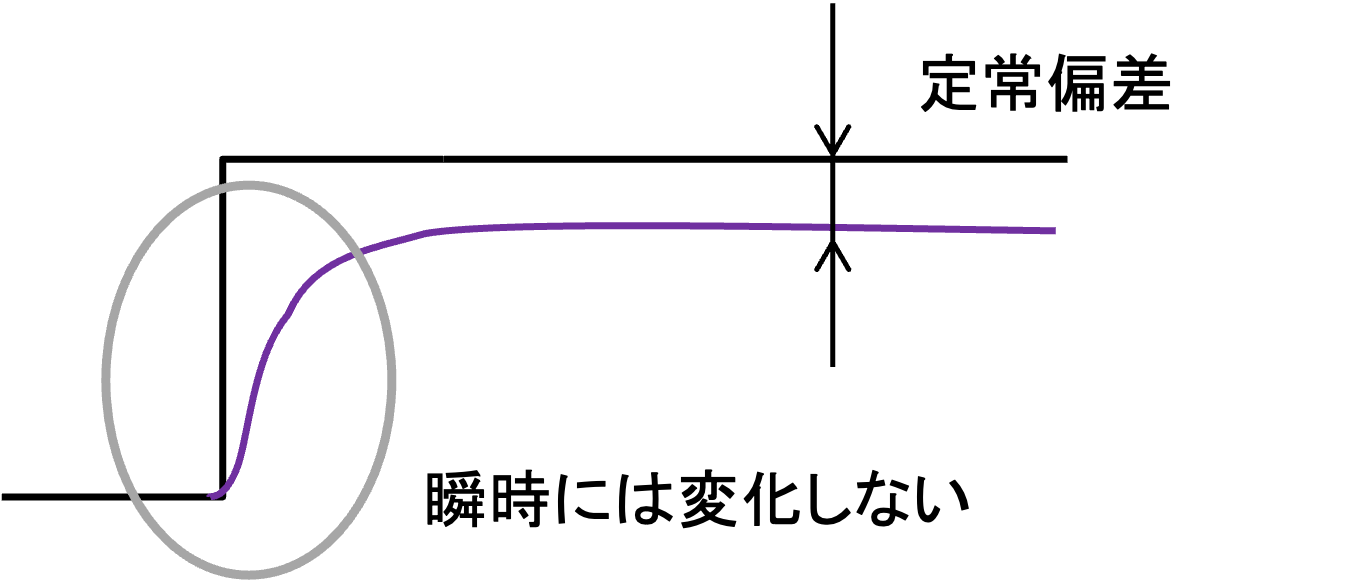
まず，目標が変化してから十分な時間が経過しても，モータ角度が目標に一致しません．このように定常的に残る偏差のことを定常偏差と言います．定常偏差もマサツなどによって生じます．比例制御は偏差の大きさに比例した制御入力（電圧）を与えます．これは，偏差が小さくなる，つまり，出力が目標に近づくほど制御入力がそのまま小さくなってしまうことを意味します．そうすると，出力が目標に一致する前に制御入力はマサツに負けてしまうので，出力は目標に到達することができなくなります（下図参照）．これによって定常偏差が生じます．

さらに，応答をよく見ると目標値が変化しても角度は瞬時には変化していないはずです．これは物体には慣性があるために角度や位置は瞬時に変化することができないためです．エレベータの位置決め制御を考えてもらえば，瞬時に位置が変化することは物理的に不可能であることが理解できると思います．モータの場合には，アームやモータ軸，モータ軸に巻かれているコイルの力学的な慣性のために，角度は瞬時には変化できません．

定常偏差が残っているので，より強力に制御するために比例ゲインを 0.08 程度に大きくしてみましょう．制御結果はよくなるでしょうか？　応答はおおよそ以下のようになっているはずです．

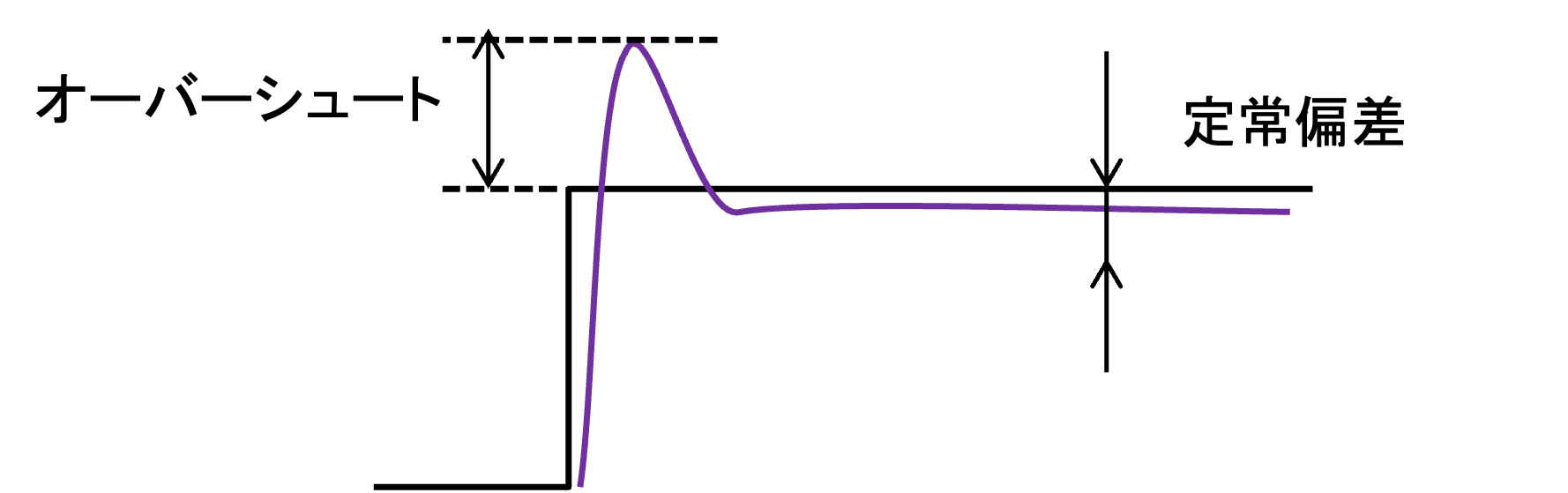
比例ゲインを大きくしたことによりモータの動きが速くなります．また，定常偏差は前よりも小さくなったはずです．一方，アーム角度は途中で目標を大きく超えるようになったはずです．アームの動きをよく見ると，アームが途中で戻ってくる様子が見えます．このように目標を超えて大きくなる部分をオーバーシュート（行き過ぎ量）と言います．オーバーシュートは目標の値に対する比率（%）で表示します．目標が１だけ変化したときにオーバーシュートが0.3の大きさだけ生じた場合には， 30%のオーバーシュートが生じたと言います．

オーバーシュートも対象の慣性によって生じます．比例ゲインを大きくしたことにより，モータは前よりも勢いよく回転するようになりました．しかしながら，モータの慣性のために一度回転し始めたモータは前よりも止まりにくくなりました．これがオーバーシュートが生じる理由です．

目標の位置を過ぎ去ってから目標に戻ってくるエレベータを想像すればわかるように，オーバーシュートは望ましくない結果です．しかしながら，オーバーシュートはしばしば生じます．

以上のように，位置決め制御ではしばしば定常偏差やオーバーシュートが生じます．実用的な位置決め制御では定常偏差は 0，オーバーシュートは5%程度未満（自動車のエンジン制御などでは0%）の性能が要求されます．そのうえで，できる限り速く目標に到達させることが求められます．これらの指標と比べると，これまでの制御結果の性能は不十分のようです．

上記のような要求を満足させるために，試しに比例ゲインを5にして実験してみましょう．振動が止まらなくなったはずです．初回の講義で体験した不安定化は，まさにこうして起きた現象です．振動が収まらなくなる現象は不安定化の一例です．

比例ゲインを0.01から0.8程度まで少しずつ変化させながら実験してみましょう．応答はオーバーシュートが生じている状況から少しずつ振動的になっていき，やがて振動が収まらなくなる様子が観察できるはずです．これら一連の様子から，不安定化がオーバーシュートが徐々に悪化していった末に起きていることが確かめられます．オーバーシュートが対象の慣性によって生じていることから，不安定化も対象の慣性が密接に関わっていると推測されます．どのように関わっているかは，今後の講義で解明されていきます．

一通り確認できたら，”stop” をクリックして実験を一時停止させておきましょう．

ファイルへの保存

制御実験の結果をファイルに保存しておきましょう．ファイルへの保存は次の手順でできます．

“stop” をクリックして実験を停止させます．
“save” をクリックします．
“data_fb_1.00000_0.00000_0.00000.csv”のようなファイルがダウンロードされるはずです．データは下記に示すようなカンマ区切りのテキスト形式にて記録されています．

ファイルの中身はデータが３列，カンマで区切られて並んでいます．一番左から時間（秒），アーム角度（Deg），目標角度（Deg），モータへの印加電圧(V)です．おおよそ 10ms ごとにデータが記録されています．

保存されたファイルは Excel を用いて開くことができます．実験結果をグラフとして表示してみてください．

データに間違いがなければ，ファイルを適当なフォルダーに保存しておいてください．このファイルから読み取れるデータがレポートに必要です．

PI制御実験

比例ゲインを大きくしていくと，定常偏差は小さくなってはいきますが0にはなりません．そのうえ，比例ゲインを大きくしすぎると制御系は不安定になってしまいます．よって，比例制御では定常偏差を0にすることはできません．

既に説明したように，定常偏差は発生するトルクがマサツで相殺されることによって生じます．比例制御では，マサツに負けても，その状況を改善することができません．マサツがあっても定常偏差を0にするためには，定常偏差が生じていたら，それに応じてトルクを大きくしていくしくみが必要です．例えば，定常偏差が生じていると偏差の積分の値は増加していくので，これを \(u(t)\)の計算に組み込めば定常偏差を0にすることができるかもしれません．

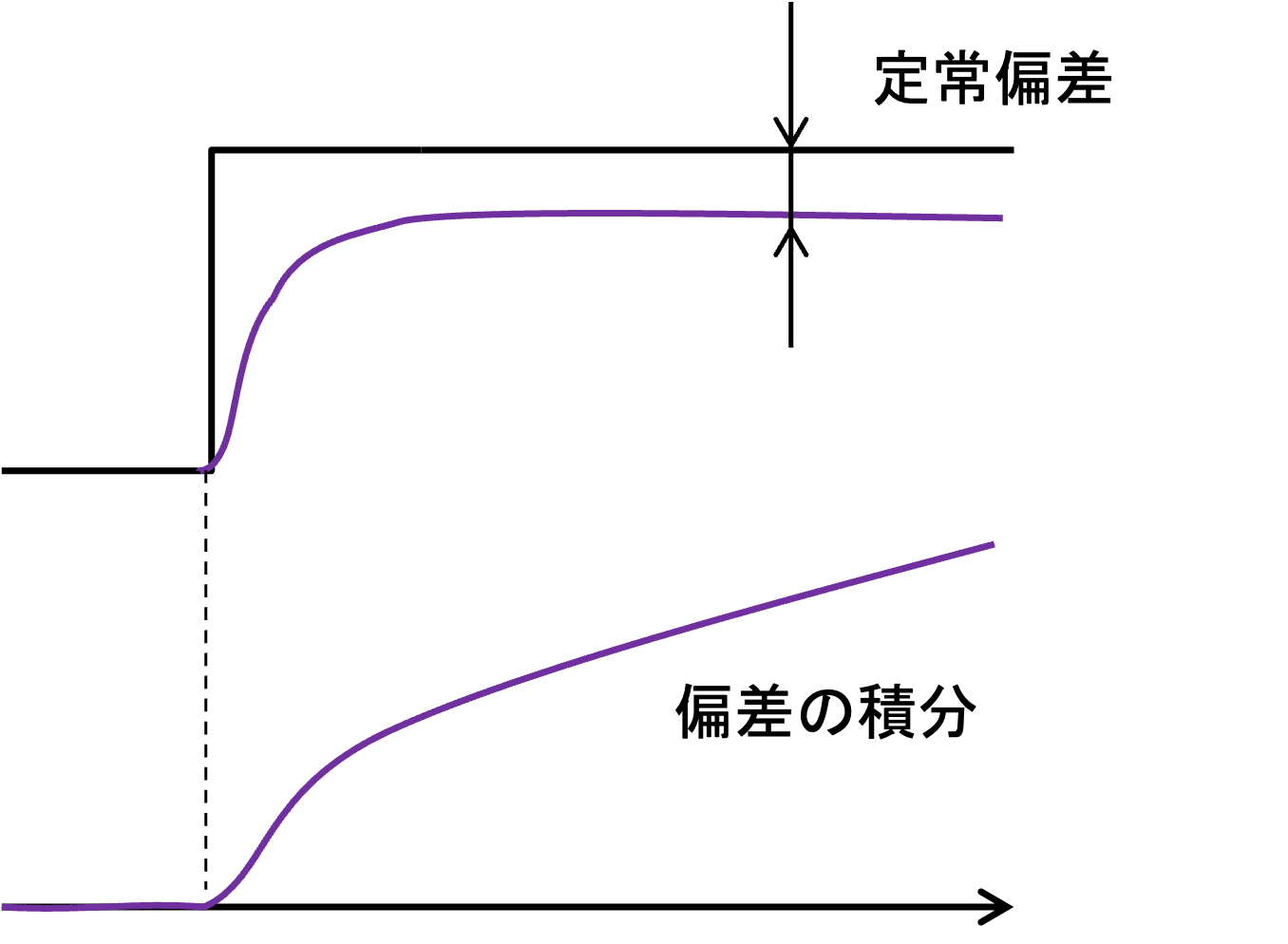
偏差の積分を利用する制御を積分制御，あるいは Integral （積分）の頭文字をとって I制御とも言います．具体的には以下の式に基づいて制御入力を定めます． \(K_i\) は比例定数で，とくに積分ゲインとよばれています．

\[\Large{ \begin{align} u(t) = K_i \int_0^t e(\tau) d\tau \end{align} }\]

実際には積分制御は比例制御と併用して用いられます．制御則は以下のものを用います．このような制御を比例積分制御あるいは PI 制御と言います．

\[\Large{ \begin{align} u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau \end{align} }\]

PI 制御の実験を行ってみましょう．実験画面の比例ゲインを 0.05 にします．積分ゲインは ”I gain” の欄で設定します．積分ゲインを 0.1 に設定して下さい．設定後に “start” をクリックすると実験が始まります．比例制御だけの場合とは異なり，時間がたつと偏差が減少していくことが確認できます．このように制御則の自由度を増やすと，それに応じて実現できる機能は増加する傾向にあります．

結果を見ると目標の場所によって応答が異なります．これは回転の方向が逆転するときにギアのバックラッシュの影響を大きくうけるためです．今考えている制御則ではバックラッシュの影響を取り除くことは困難なので，今回の実験に限っては目標の場所による応答の違いは気にしなくても構いません．

比例ゲイン，積分ゲインをいろいろ変えて実験を行い，各制御ゲインの効果を確かめてみましょう．

PD制御実験

これまでに比例制御，積分制御を導入しました．積分と言えば微分をすぐに連想すると思いますが，微分を用いた制御もよく用いられます．まずは，制御則は以下のものを用いてみましょう．このような制御を微分制御，あるいはPD制御と言います． D は Derivative（微分）の頭文字です．\(K_d\) は微分ゲインとよばれます．

\[\Large{ \begin{align} u(t) = K_p e(t) + K_d \frac{d}{dt} e(t) \end{align} }\]

微分制御は偏差の微分に基づいて制御を行うので，偏差が大きく変化するときに大きな値を出力します．目標値が急に変化したときには偏差が大きく変化するので，微分制御は目標値が変化するときに制御対象をいち早く動かす，すなわち初動をすばやくさせることに役立ちます．逆に，偏差が小さくなると出力を小さくさせるので，振動的な挙動を抑えることに役立ちます．しかしながら一方で，微分制御はノイズのようなすばやく変化する要因を増幅してしまうデメリットも併せ持っています．

微分ゲインは実験画面の “D gain” の欄で設定します．最初は 0.01 程度の値から始めてみましょう．

PID制御実験

これまでに比例制御，積分制御，微分制御を導入しました．この三つを用いた制御則を，PID制御と言います．制御則は以下のものを用います．

\[\Large{ \begin{align} u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{d}{dt} e(t) \end{align} }\]

制御性能は PID ゲイン（\(K_p, K_i, K_d\)）の値に依存します．PID ゲインを変えながら，できる限り望ましい性能を達成するような制御則を探して下さい．結果として先に挙げた位置決め制御系に対する要求が達成できれば理想的です．ただし，必ずしもその要求を達成できるとは限りません．今回の実験は制御系設計の難しさを実感することも目的としています．今後の講義の中で徐々に必要な事柄を学んでいきますので今の段階でうまくできなくても構いません．しかし，それでもできる限り高い性能を目指して下さい．

レポート課題

以下の内容をまとめてレポートを提出しなさい．レポートは1週間後の13:00までにCLEにて提出するように. なお，考察においては，オーバーシュートと定常偏差の用語を用い，定量的な評価を行うこと．

\(K_p\)を変えながら，P制御（\(K_i= K_d=0\) ）を用いて実験を行い，その際の実験結果をプロットした図を記しなさい．そして，実験結果をもとに，P制御の特徴について考察しなさい．
\(K_p\)を固定し\(K_i\)を変えながら，PI制御（\(K_d=0\)）を用いて実験を行い，その際の実験結果をプロットした図を記しなさい．そして，実験結果をもとに，PI制御の特徴について考察しなさい．
\(K_p\)を固定し\(K_d\)を変えながら，PD制御（\(K_i=0\)）を用いて実験を行い，その際の実験結果をプロットした図を記しなさい．そして，実験結果をもとに，PD制御の特徴について考察しなさい．
PIDゲインをいろいろ変えながら，PID制御を用いて実験を行い，その際のPIDゲインと実験結果をプロットした図を記しなさい．そして，実験結果について考察しなさい．