第4回実験
はじめに
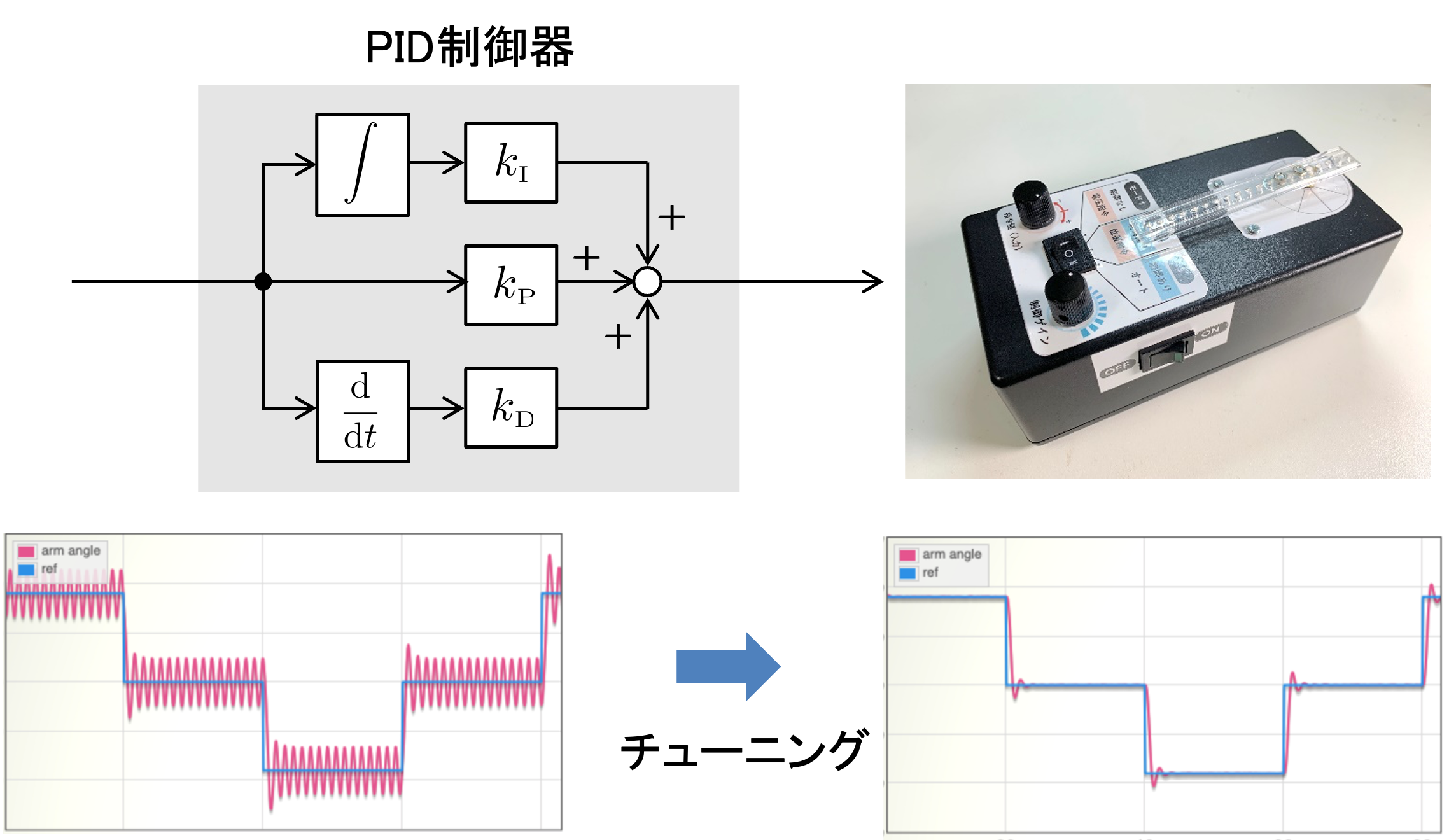
今回の実験のテーマは「PID制御器のゲインチューニング」です. 第一回の実験では,PID制御について学び, そして試行錯誤的にゲインチューニングをしました. 今回は,それをシステマティックに行う方法を体験します.
まず,「限界感度法」と呼ばれる実験データを用いてゲインチューニングを行う方法を学びます. つぎに,「部分的モデルマッチング法」と呼ばれる制御対象のモデル情報 (モデルの求め方は第二回,第三回の実験で学びました)を用いて,ゲインチューニングを行う方法を学びます.
PID制御とI-PD制御
PID制御は,比例制御,積分制御,微分制御を組み合わせたものです.制御則はつぎのとおりです. ただし,\(e\) は目標値と出力の差(偏差)\(e = r - y\) です.
\[\Large{ \begin{align} u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{d}{dt} e(t) \end{align} }\]ブロック線図は以下のようになります.
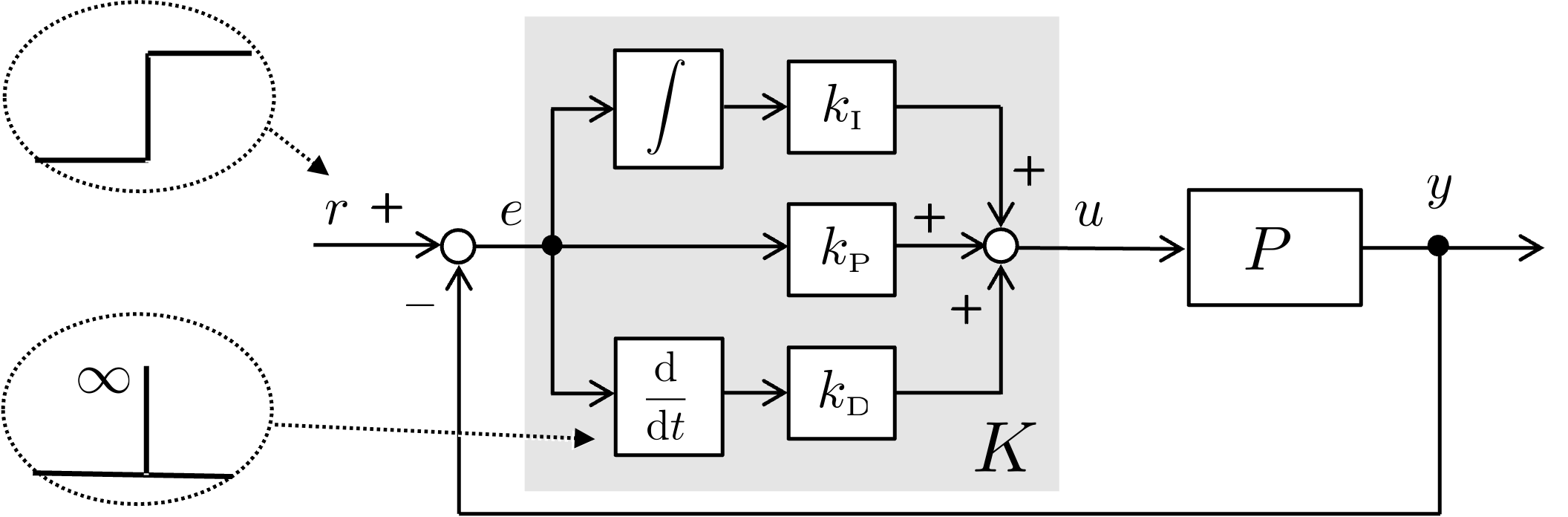
PID制御では,偏差 e の微分情報を利用しますが,目標値 r がステップ信号のように, 急激に変化する場合には,偏差の微分はとても大きな値になります. これは,制御入力 u が過大になり, 応答が振動的になる可能性があることを意味しています. そのため,改良版PID制御が用いられることが多いです.
具体的には,比例制御と微分制御を出力yの情報を用いて行うようにした I-PD制御(比例・微分先行型PID制御)がよく用いられます.
\[\Large{ \begin{align} u(t) = -K_p y(t) + K_i \int_0^t e(\tau) d\tau - K_d \frac{d}{dt} y(t) \end{align} }\]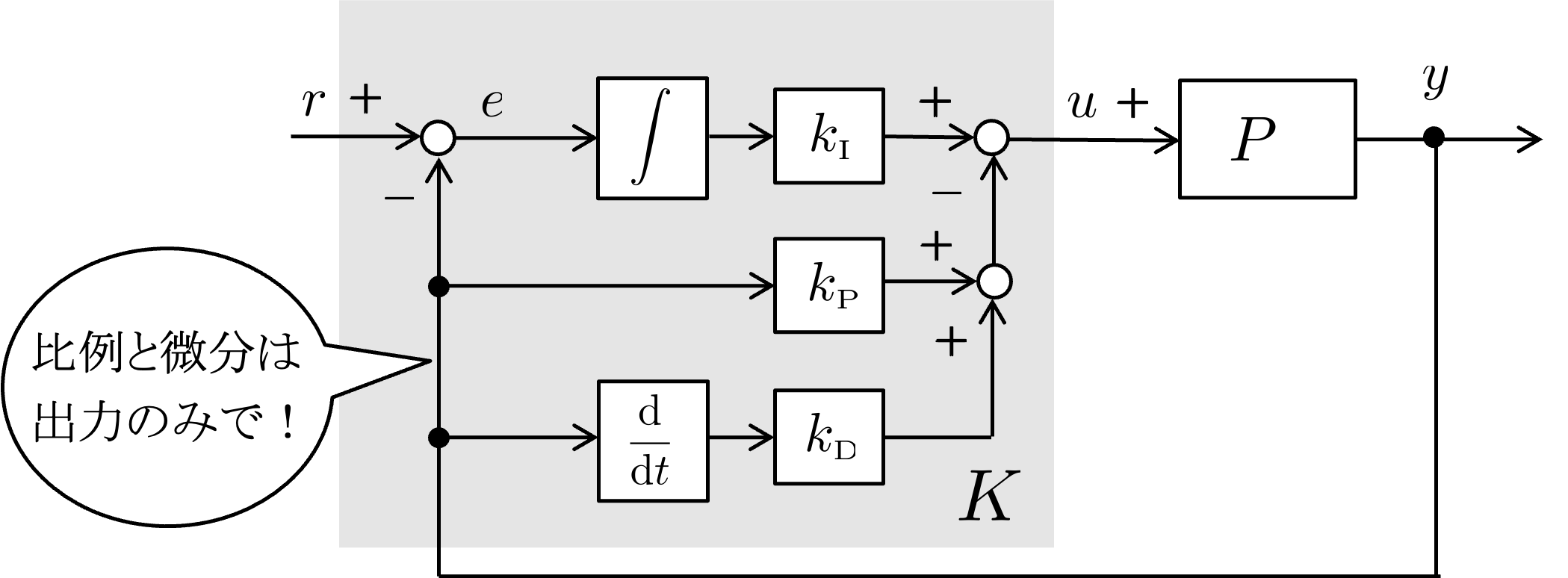
限界感度法
限界感度法は,制御対象のモデルを用いず,実験データからゲイン調整を行うものです. 実験ができれば,そこそこのゲイン調整が可能です. 一方,実験を繰り返す必要がある点や,安定な制御対象に限定される点, 限界感度(不安定になる手前)付近で実機を動かす必要がある点などが欠点となります.
限界感度法では,まず,P 制御を施して閉ループ系を構成し,比例ゲイン 𝑘_𝑃 を大きくしていきます.すると,振動が大きくなり,制御対象によっては,持続振動が生じます.1次遅れ系や2次遅れ系では,理論的には,振動は生じません.しかし,現実には,微小な遅れや振動モードがありますので,それによって振動が生じます.
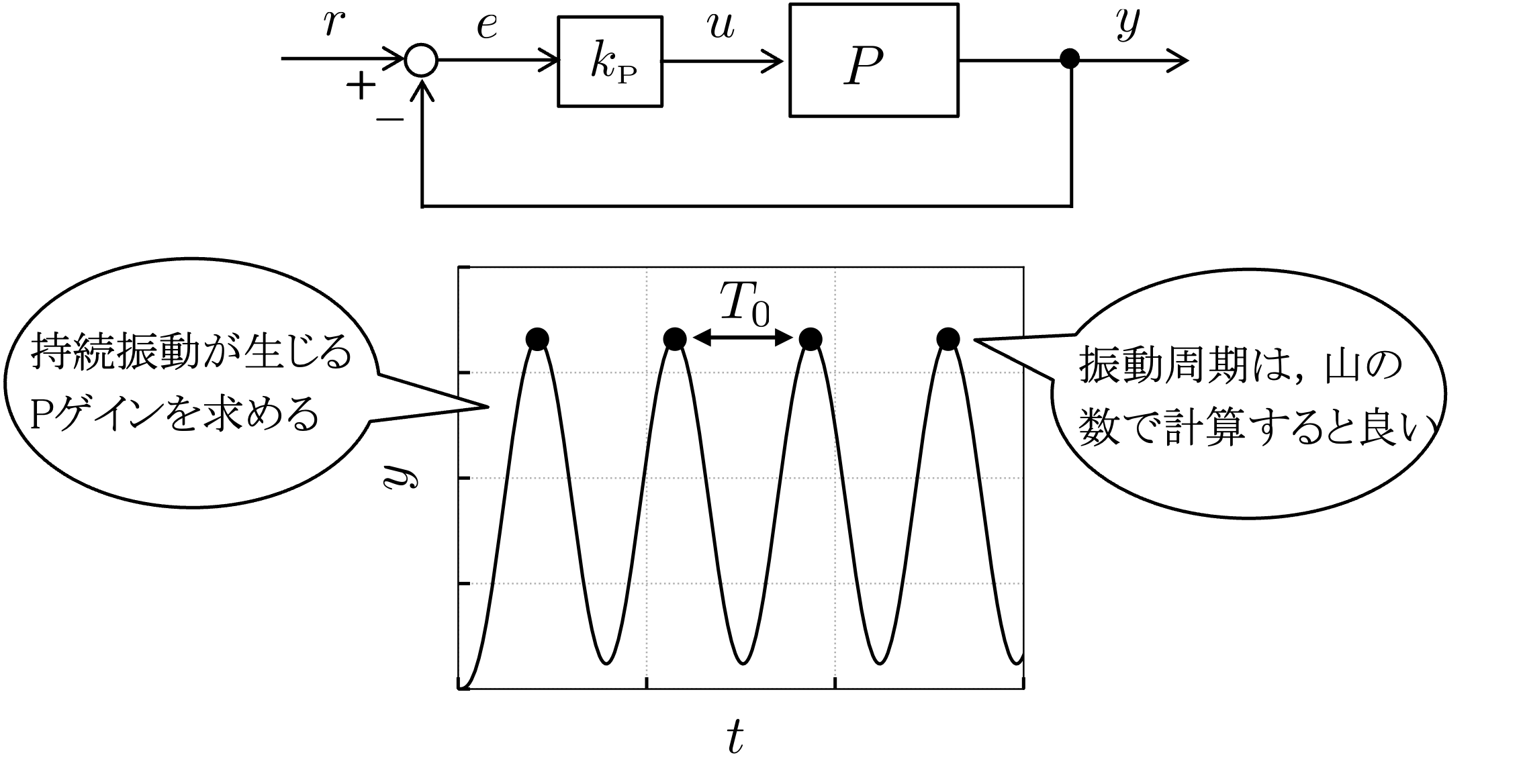
持続振動が生じたときの比例ゲイン\(k_{P0}\)と持続振動の周期\(T_0\)を用いて, PIDゲインを以下の表を利用して決定します. 表中の\(k_I\)や\(k_D\)の値を決定する\(k_P\)は\(k_{P0}\)と異なることに注意してください.
| \(k_{P}\) | \(k_{I}\) | \(k_{D}\) | |
|---|---|---|---|
| PID制御 | \(0.2k_{P0}\) | \(k_{P}/(0.5T_{0})\) | \(0.33k_{p}T_{0}\) |
限界感度法によるゲイン調整
Feedback制御実験を開いてください.別タブで開きます.
まずは,“connect”をクリックし,実験装置が接続されているUSBポートを選択します.Windowsの場合は,”COM**“,Macの場合は,”/dev/cu.usbserial” などが選択できると思います.できない場合は,接続を確認してください.
実験手順
1. 目標軌道をステップ入力にします.
2. 積分ゲイン(I gain)と微分ゲイン(D gain)を0にします. そして,比例ゲイン\(k_P\)を0.1から徐々に大きくしていき, 持続振動を生じさせます. 表示されているプロットは全てのデータを表示しているわけではないため(高周波の振動は表示されません), 実験機の方で,持続振動が起きているか確認してください. (保存されるデータには,全てのデータが記録されています)
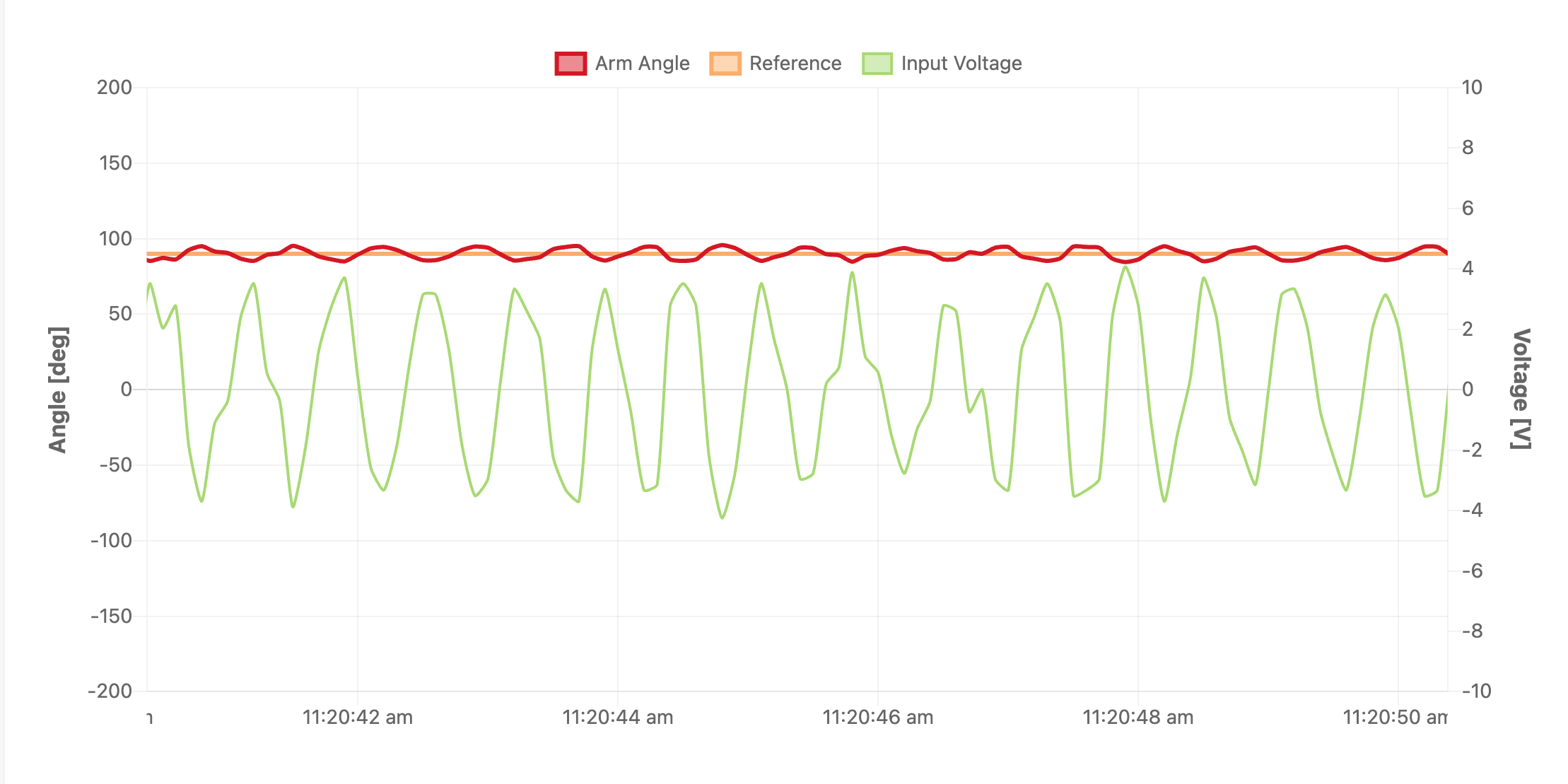
3. 持続振動が起こったときの比例ゲイン\(k_{P0}\)と周期\(T_0\)の値を記録します.
4. そして,表1より,PIDゲインを求めます.
5. 求めたPIDゲインの値をゲイン設定ボックスに入力します.
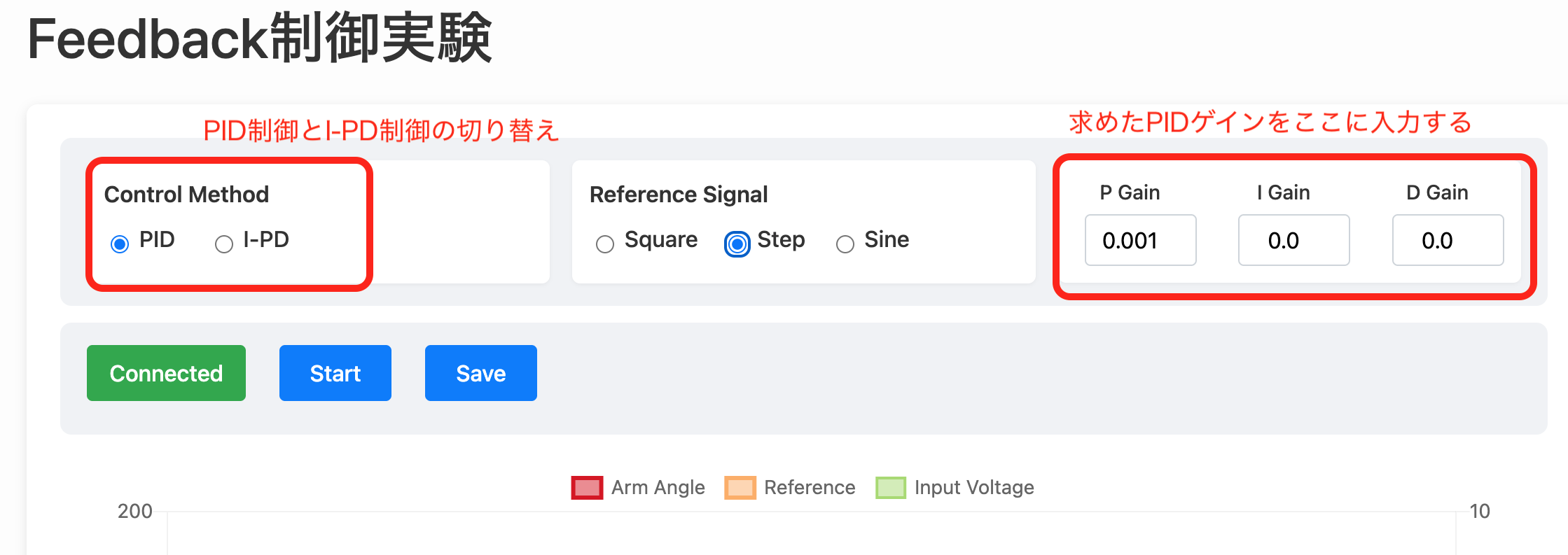
5. ”start/stop”ボタンによって実験を開始し,応答を確認しましょう. さらに,”save”ボタンで実験データを記録しましょう.
6. 最後に,I-PD制御の実験をします.ゲインはそのままで, ”I-PD” にチェックを入れて,実験を開始し,応答を確認しましょう.
ファイルへの保存
制御実験の結果をファイルに保存しておきましょう.ファイルへの保存は次の手順でできます.
- “stop” をクリックして実験を停止させます.
- “save” をクリックします.
- “data_fb_1.00000_0.00000_0.00000.csv”のようなファイルがダウンロードされるはずです.データは下記に示すようなカンマ区切りのテキスト形式にて記録されています.

ファイルの中身はデータが3列,カンマで区切られて並んでいます.一番左から時間(秒),アーム角度(Deg),目標角度(Deg),モータへの印加電圧(V)です.おおよそ 10ms ごとにデータが記録されています.
保存されたファイルは Excel を用いて開くことができます.実験結果をグラフとして表示してみてください.
データに間違いがなければ,ファイルを適当なフォルダーに保存しておいてください.このファイルから読み取れるデータがレポートに必要です.
モデルマッチング法
モデルマッチング法は,ある適切な規範モデル\(M(s)\)を与え, それに目標値\(r(s)\)から制御量\(y(s)\)までの 伝達関数\(G_{yr}(s)\)を一致させる (または近づける) というものです. この方法では,制御対象のモデル情報\(P(s)\)を利用します.
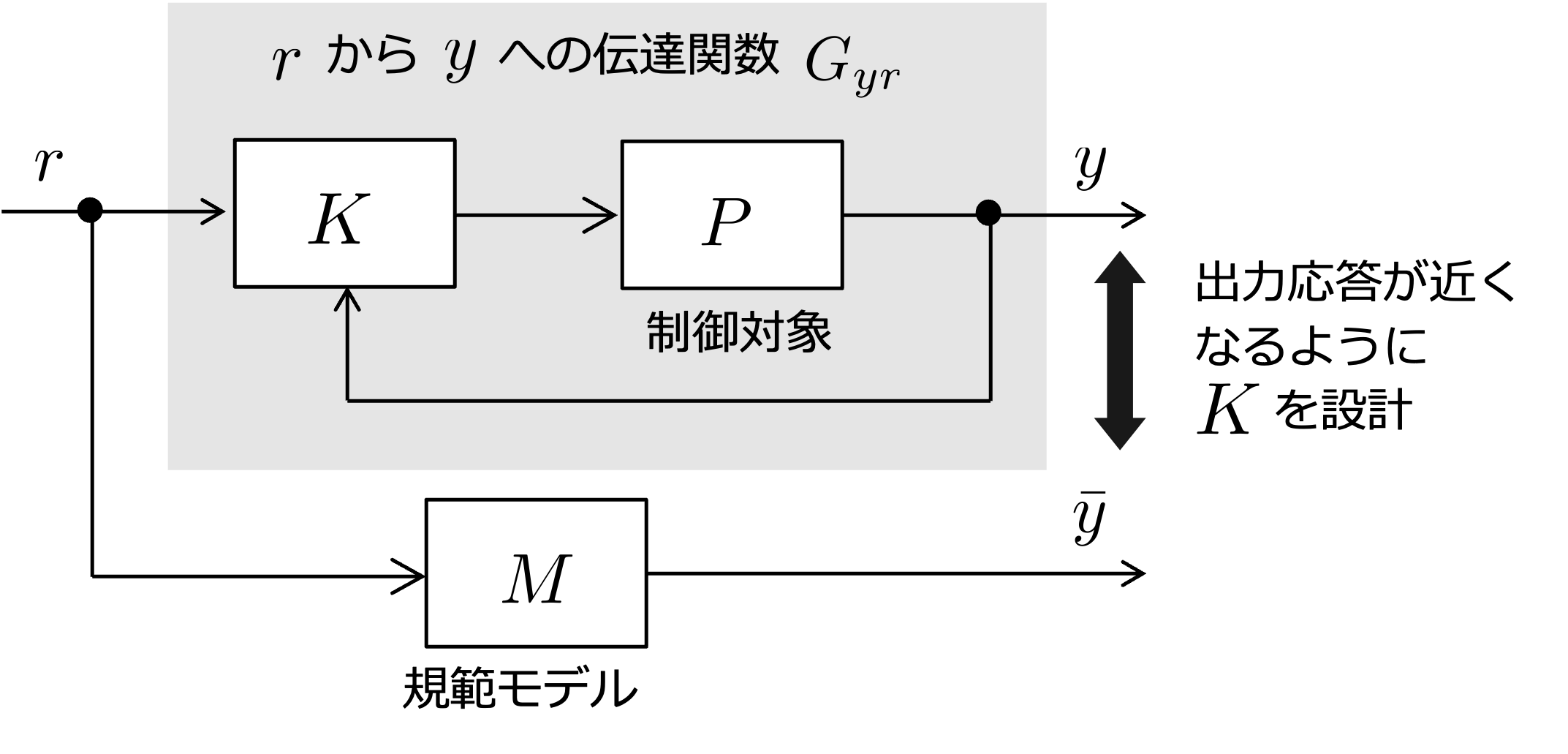
部分的モデルマッチング法(北森法)
ここでは,PIDゲインをシステマティックに算出できる部分的モデルマッチング法(北森法)を利用します.
まず, \(r(s)\) から \(y(s)\) への伝達関数\(G_{yr}(s)\)を求め, \(1/G_{yr}(s)\)のマクローリン展開 ( 0 を中心としたテイラー展開)を計算し,\(s\) の多項式を求めます.
\[\Large{ \begin{align} \frac{1}{G_{yr}(s)} = \gamma_0 + \gamma_1 s + \gamma_2 s^2 + \cdots \end{align} }\]さらに,規範モデル\(M(s)\)に対して, \(1/M(s)\) のマクローリン展開を計算し,\(s\)の多項式を得ます.
\[\Large{ \begin{align} \frac{1}{M(s)} = \delta_0 + \delta_1 s + \delta_2 s^2 + \cdots \end{align} }\]上記の二つの多項式の係数を低次の項から順に一致させるように,PID ゲインを決定します. このようにすることで,制御対象の出力が規範モデルの出力に完全に一致します(または,近くなります).
モデルマッチング法によるゲイン調整
ここでは,モータのモデルが以下のように求まっているとします (第二回,第三回の実験で,モータのモデルを求めました).
\[\Large{ \begin{align} P(s) = \frac{b}{s(s+a)} \end{align} }\]モータにI-PD制御を施すと,目標値から出力までの伝達関数\(G_{yr}(s)\)は,以下のようになります.
\[\Large{ \begin{align} G_{yr}(s) = \frac{bk_I}{s^3 + (a+bk_D)s^2 + bk_P s + bk_I} \end{align} }\]閉ループ系の伝達関数\(G_{yr}(s)\)を3次の規範モデル
\[\Large{ \begin{align} M(s) = \frac{\omega_n^3}{s^3 + \alpha_2 \omega_n s^2 + \alpha_1 \omega_n^2s + \omega_n^3} \end{align} }\]に一致させるように,PIDゲインを求めます(各自で計算してください).
ただし,
- 制御対象のパラメータを\(a=31, b=6616\)とします.
- 規範モデルのパラメータを
- \(\omega_n = 25\), \(\alpha_1 = 2\), \(\alpha_2 = 2\) (バターワース標準形)
- \(\omega_n = 25\), \(\alpha_1 = 3\), \(\alpha_2 = 3\) (二項係数標準形)
- \(\omega_n = 15\), \(\alpha_1 = 3\), \(\alpha_2 = 3\)
と設定して,PIDゲインを計算し,実験を開始してください.(I-PD制御で実験をしてください.)
レポート課題
以下の内容をまとめてレポートを提出しなさい.レポートは一週間後の13:00までにCLEにて提出するように. 実験結果はグラフだけでなく,PIDゲインの値および,その計算過程も報告すること.
1. 限界感度法を用いてPIDゲインを調整し,追従制御実験を行う. PID制御とI-PD制御の2通りの実験を行い(ゲインは同じ), それらの違いを考察せよ. なお,PID制御の応答の振動が大きくなりすぎる場合には, Iゲインを半分の値に設定するなど適宜微調整してよい。
2. 制御対象が
\[\Large{ \begin{align} P(s) = \frac{6616}{0.01s^3 + s^2 + 31s} \end{align} }\]であるとする.このとき,P制御系が安定限界となる\(k_P\), つまり,一巡伝達関数\(k_P P(x)\)のベクトル軌跡が -1を通る\(k_P\)を計算で求めよ. さらに,それと限界感度法の実験でもとめた\(k_{P0}\)と比較せよ.
3. モデルマッチング法を用いてPIDゲインを調整せよ. ただし,制御対象のモデルは,
\[\Large{ \begin{align} P(s) = \frac{6616}{s^2 + 31s} \end{align} }\]であるとし,制御器はI-PD制御器とする. また,規範モデルは3次系とし,パラメータは,
- \(\omega_n = 25\), \(\alpha_1 = 2\), \(\alpha_2 = 2\)
- \(\omega_n = 25\), \(\alpha_1 = 3\), \(\alpha_2 = 3\)
- \(\omega_n = 15\), \(\alpha_1 = 3\), \(\alpha_2 = 3\)
とする.追従制御実験を行い,結果の違いを考察せよ(とくに,極と応答の関係,理想的な応答との差異などを考えよ).
付録1 モデルに関する補足
第二回,第三回の実験では,モータのモデルを2次系として求めましたが,今回の実験(前半)では,モータが3次系であるとしました.これは,以下のように考えるとよいでしょう.
考え方1
モータのインダクタンスを無視(\(L=0\))とすると, 印加電圧から出力角度までの伝達関数は2次系となります.
\[\Large{ \begin{align} P(s) = \frac{K}{Js^2 + Bs} \end{align} }\]一方,インダクタンスを無視しなければ,3次系となります.
\[\Large{ \begin{align} P(s) = \frac{K}{(LJ/R)s^3 + (J+LD/R)s^2+Bs} \end{align} }\]考え方2
微小なむだ時間\(h\)がある場合は,2次系+むだ時間要素となります.
\[\Large{ \begin{align} P(s) = \frac{K}{Js^2 + Bs}e^{-hs} \end{align} }\]むだ時間要素は,パディ近似により,有理関数で記述できます.
\[\Large{ \begin{align} P(s) = \frac{K}{Js^2 + Bs} \times \frac{2-hs}{1+hs} \end{align} }\]なお,第三回の実験で,制御対象の位相が-180度を下回る結果が得られることがありましたが,これは,制御対象が3次系やむだ時間要素であったと考えれば,理解できると思います.
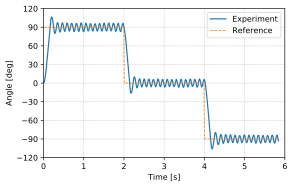
付録2 Pythonでグラフ作成
import numpy as np
import matplotlib.pyplot as plt
# data.csvファイルの中身を読み込んでaに保存
a = np.loadtxt('data.csv', delimiter=',')
# グラフのサイズを指定する
fig, ax = plt.subplots(figsize=(5.5, 3.5))
# aの一列目と二列目でグラフを作成
ax.plot(a[:,0], a[:,1], label='Experiment')
# aの一列目と三列目でグラフを作成
ax.plot(a[:,0], a[:,2], ls='--', lw=1, label='Reference')
ax.set_xlim([0, 6]) #横軸のレンジ
ax.set_ylim([-120, 120]) #縦軸のレンジ
ax.set_xticks(np.arange(0, 7, 1)) #横軸の目盛り
ax.set_yticks(np.arange(-120, 121, 30)) #縦軸の目盛り
ax.set_xlabel('Time [s]') #横軸のラベル
ax.set_ylabel('Angle [deg]') #縦軸のラベル
ax.legend(loc='best') #凡例を適当な位置に配置
ax.grid(ls=':') #グリッドの表示(破線)
fig.savefig('zn_exp.pdf',bbox_inches='tight')