第3回実験
はじめに
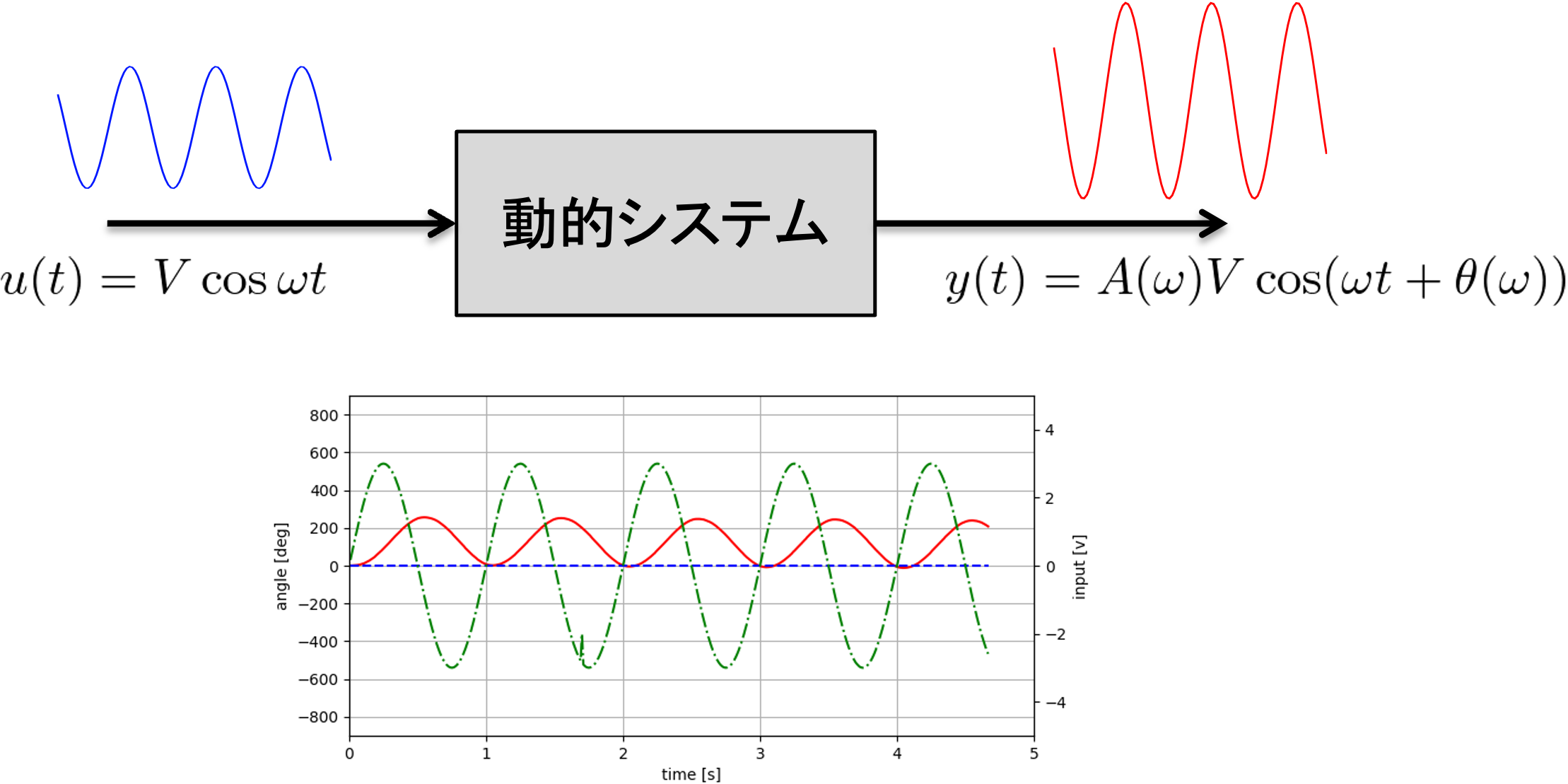
今回の実験のテーマは「動的システムの周波数特性」です.システムに信号が入力されたときに,各周波数成分がどのように増幅・減衰され,また遅れて出力されるかを調べます.実験では「DCモータ」を題材とし測定を行います.
第三回コア実験も資料と説明動画を見ながら,ブラウザ上で動く実験機のシミュレータを用いて各自で進めてください. シミュレータは こちらに準備しています.
インパルス入力と余弦波入力
インパルス入力に対する応答(インパルス応答)がわかれば,様々な入力に対する応答が計算できます.しかしながら,インパルス入力は時刻\(t=0\)において無限大の大きさを持つ信号であり,実際のシステムに印加することはできません.
そこで,インパルス関数が余弦波の集まりであることに着目し,
\[\large{ \delta(t) = \int_{-\infty}^{\infty} \cos \omega t d\omega \approx \sum_{n=-\infty}^{\infty} \cos \omega_n t \frac{\omega_n}{2\pi} }\]様々な余弦波入力の応答を測定することで,システムの特性を調べます. (実際には正弦波入力に対する応答を調べますが,原理は同じです)
安定なシステムについては,余弦波入力に対する応答も余弦波になります.

その際,
- 角周波数 \(\omega\)[rad/s] は不変
- 振幅は \(A(\omega)\) 倍
- 位相が \(q(\omega)\) [rad] ずれる(遅れる) ことになります.
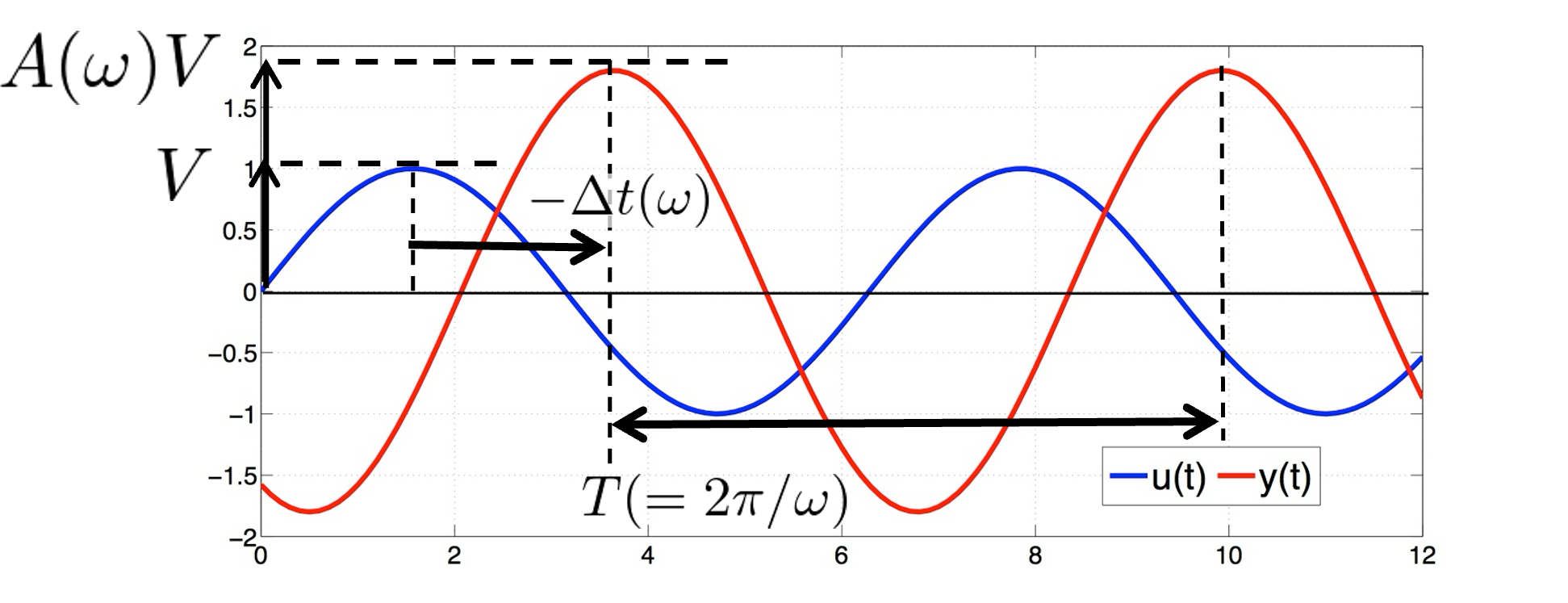
(注)位相差\(q(w)\)は,入力,出力信号がピーク値をとる時間の差を\(-Dt(w)\), 信号の周期を\(T(=2\pi/w)\)とすると,\(q(w) = - 360× Dt (w) / T [deg]\)
ゲイン特性と位相特性
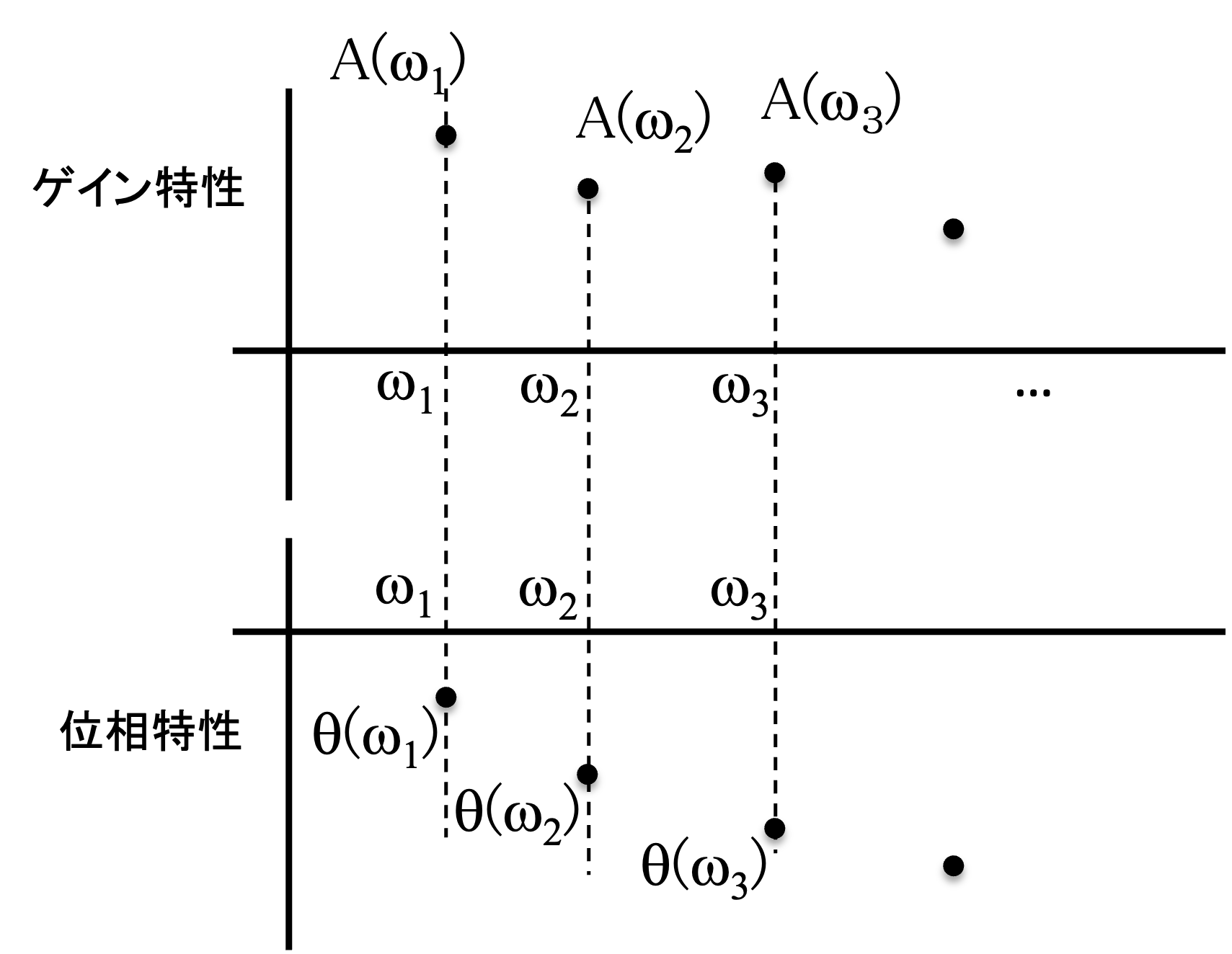
このA(w),q(w)はそれぞれゲイン特性,位相特性と呼ばれ,動的システムのの特性(信号の伝達具合)を表すものとなります.さらにその両者を用いた,
\[\large{ G(j\omega) = A(\omega) e^{j q(\omega)} }\]は,周波数伝達関数と呼ばれます.
本実験では,様々な周波数の信号を動的システムに入力し, その応答を計測して,ゲイン特性\(A(\omega)\),位相特性\(\theta(\omega)\)を求めます.

ボード線図
ボード線図は,ボード(Bode)によって1930年代に考案され, 実際の制御系設計において広く用いられている非常に重要なものです.
ボード線図は角周波数 \(\omega\) rad/s に対するゲイン特性 \(|A(\omega) |\)の変化を表すゲイン曲線, 位相特性 \(\theta(\omega)\) の変化を表す位相曲線 からなります.
横軸に角周波数\(\omega > 0\) を対数目盛りで表し, 縦軸は,ゲイン曲線はデシベル値 dB, つまり \(20\log10|A(\omega)|\),位相曲線は度[deg]で表します.
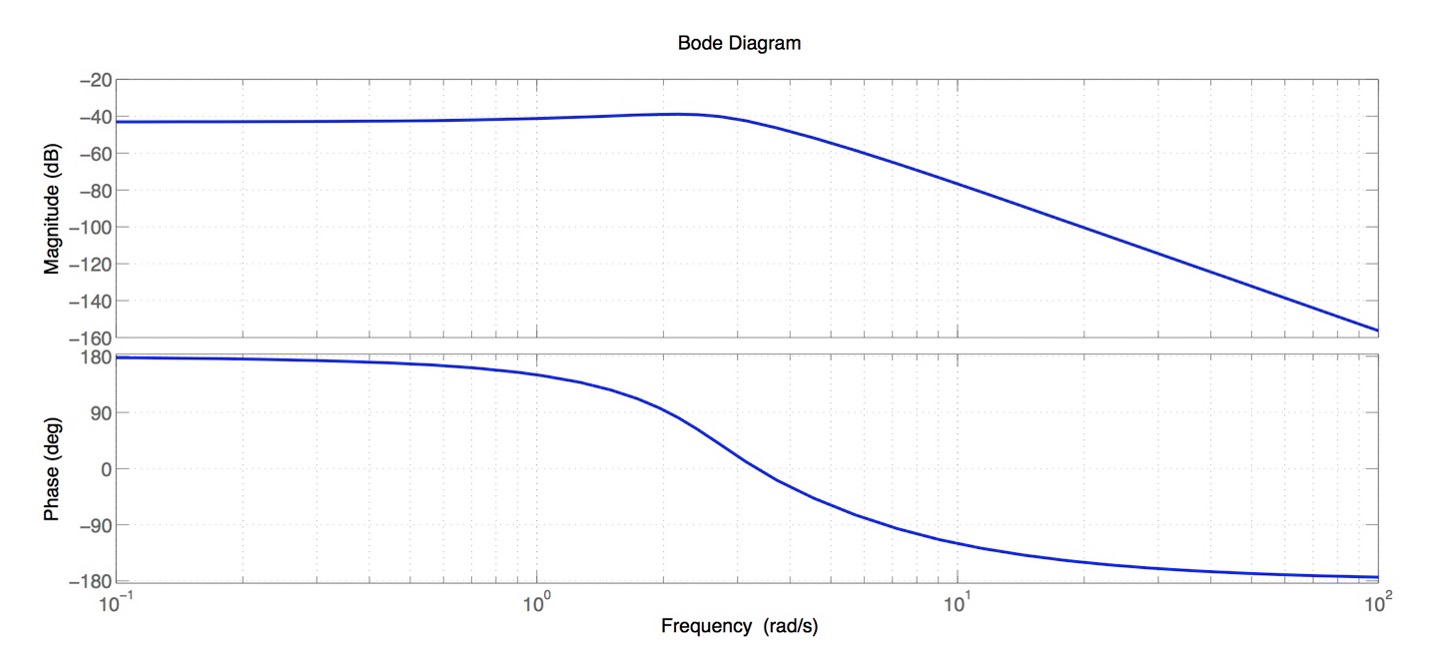
なお角周波数については,数学的には rad/s を用いた方が都合がよいことが多いのですが, 音声などでは Hz = 1/s を用いる場合もあります.両者は 1 Hz = \(2\pi\) rad/s の関係にあります.
モータの周波数応答の測定
1. ”mode”にて”Feedforward”を選択し,”inputs”にて”sin”を選択してください.これにより,モータにsin波入力を与える設定になります.
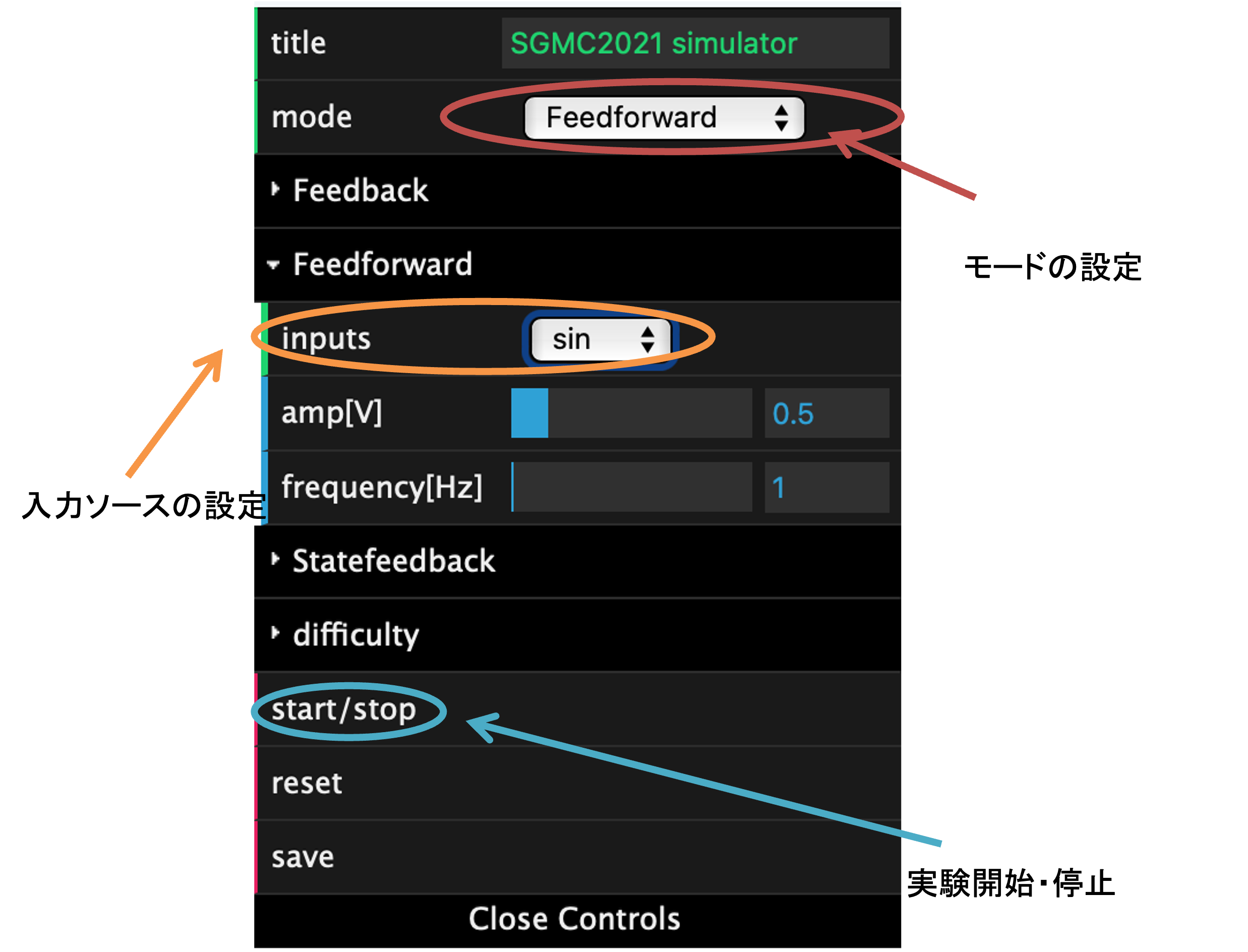
2. amp, frequencyのところに,入力の振幅電圧Vと周波数fを設定します.start をクリックすると,
\[\large{ u(t) = V \sin \omega t }\]という電圧入力が印加されます.ただし,\(\omega=2 \pi f\) [rad/s] です.
- それではモータを動かしてみましょう.“start” をクリックしてみましょう. モータが回転を始めると同時にブラウザには下図のようなグラフが表示されるはずです. 赤のグラフはアームの角度をあらわしています. 下図は,ampを3.0,frequencyを1にしたときの例です. sin波入力により,アームの角度もsin波状の応答をしていることがわかります.
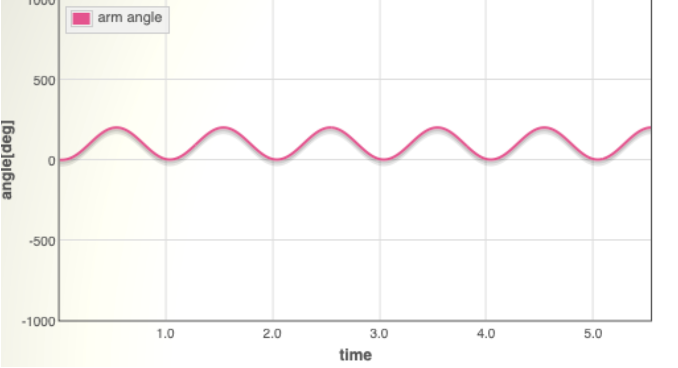
4. 測定を行ったら,“save” をクリックして制御実験の結果をファイルに保存しておきましょう. “data_ff_0.500_1.000.csv”のようなファイルがダウンロードされるはずです. データは下記に示すようなカンマ区切りのテキスト形式にて記録されますので, ファイル名は振幅電圧と周波数から自動で生成されたものになっています

5. ファイルの中身はデータが4列,カンマで区切られて並んでいます.一番左から時間(秒),アーム角度(deg),アナログ入力電圧(V),モータへの印加電圧(V) です.(ただし, “Input Signals”にて”sin”を選択した場合は,アナログ入力は使っておらず,電圧(V)は常に0になるようにしています)おおよそ 1 s ごとにデータが記録されています.
6. 周波数fを0.1〜50 Hzで適宜変化させ,実験を繰り返してください(レポート課題1)
レポート課題
以下の内容をまとめてレポートを提出しなさい.レポートは一週間後の13:00までにCLEにて提出するように.
1. 周波数\(f\)を0.1〜50 Hzで適宜変化させながら,正弦波入力
\[\large{ u(t) = V \sin \omega t }\]に対するモータの応答
\[\large{ y(t) = A(\omega) V \sin (\omega t + \theta(\omega)) }\]を測定せよ. その結果から,ゲイン特性\(A(\omega)\)と位相特性\(\theta(\omega)\)を読み取り, それらをプロットしたボード線図(ゲイン線図と位相線図の両方)を作成せよ.
2. モータの回転角を\(\theta\),角速度を\(\omega\), 電圧入力を\(e\)としたときの,モータのモデル(下式)から, \(e\)から\(\theta\)への伝達関数を\(J\), \(B\), \(K\)を用いて表せ. そして,求めた伝達関数のボード線図を作成し,1の結果と比較し考察せよ.
\[\large{ J\ddot{\theta} + B\dot{\theta} = K e }\] \[\large{ \theta(s) = \int_{0}^{t} \omega(\tau) d\tau }\]3. 白色雑音とインパルス信号は,「低域から高域まで全ての周波数成分を含む信号」という点で共通している. では,その相違点は何かを考察せよ.